旺崽的博客

要么天赋异禀，要么天道酬勤

0%

2021牛客寒假算法基础集训营1 E.三棱锥之刻

发表于 分类于 Valine：

题目链接

题目描述

牛牛站在一个棱长为的正三棱锥内部的中心。（牛牛是不可移动的）
（所谓正三棱锥，指六条棱都相等的三棱锥。正三棱锥的中心指到 4 个顶点距离都相等的那个点）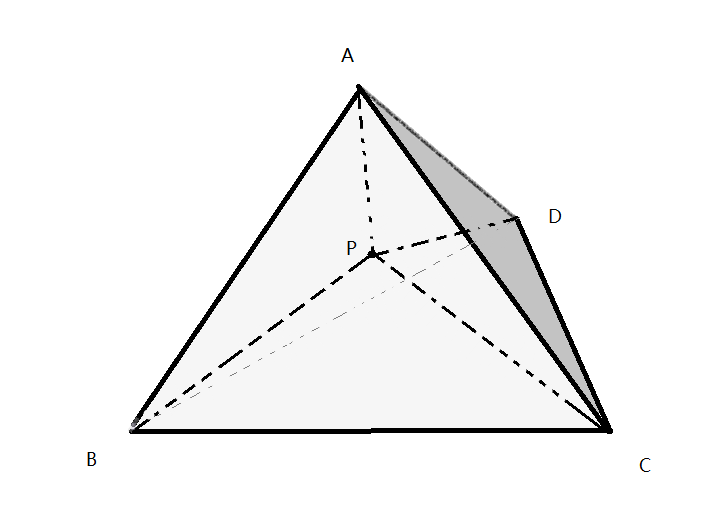
在这里插入图片描述

如上图，$AB=AC=BC=AD=BD=CD=a$，牛牛站在P点，$PA=PB=PC=PD$
他拿着一个染色喷雾，可以用来给正三棱锥的内表面染色。
已知喷雾能喷洒的距离为。也就是说，三棱锥内表面距离牛牛不超过的点才有可能被染色。牛牛想知道，正三棱锥内表面能被他染色的最大面积是多少？
ps：牛牛可看成一个无大小的点。重力对于喷雾的影响忽略不计。

输入描述:

两个正整数和
$1 \leq a, r \leq 1000$

输出描述:

染色的最大面积。若你的答案和正确答案误差不超过 $1 \times 10^{-3}$
，则认为你的答案正确。

示例1

输入

1
1 1

输出

1
1.73205

这题就是简单几何，实际上就是球体和三棱锥相交的表面积，粗略画一下图发现很简单，就 $3$ 种情况：

  • 喷洒距离 $r$ 小于正四面体内接圆的半径，此时答案为 $0$
  • 喷洒距离 $r$ 小于正四面体外接圆的半径，大于等于内接圆的半径，这种情况有两种可能，一种是整个圆内含于三角形，此时的喷射面积就是四个圆的面积；另一种可能就是圆与三角形相交，下图展示一个面的情况
  • 喷洒距离 $r$ 大于等于正四面体外接圆的半径，此时答案就是正四面体的表面积

在这里插入图片描述
显然难点就是算这个相交部分的面积了，相交部分的面积我们就用三角形的面积减去三个类三角形的面积即可，我们可以对一个角进行分析，如下图：
在这里插入图片描述

类三角形的面积=上三角形的面积-(扇形面积-下三角形的面积)
我们设几个参数名：

  • 相交部分面积 $ans$
  • 内接圆半径 $mn$
  • 外接圆半径 $mx$
  • 下三角形面积 $S1$，底 $A$，高为 $H$，斜边长 $L$
  • 上三角形面积 $S2$，底 $A$
  • 扇形面积 $S3$，对应弧长 $l$，圆形角 $\alpha$

下三角形的斜边长为：

可以通过反三角函数先算出角 $p$ 的大小：

那么：

那么圆形角 $\alpha$ 为：

所以弧长既可以计算如下：

所以扇形面积：

下三角的底 $A$ 为：

下三角的高 $H$ 为：

所以：

上三角形是很明显是一个等边三角形，面积为：

最后答案就是：

那最后的答案就是 $4*ans$，AC代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <bits/stdc++.h>

typedef long long ll;
using namespace std;
#define PI acos(-1)
double a, r;

int main() {
    cin >> a >> r;
    double mx = sqrt(6) / 4 * a, mn = sqrt(6) / 12 * a, mid = sqrt(2) / 4 * a;
    if (r < mn) printf("0.00000\n");
    else if (r < mid) {
        printf("%.5f\n", 4 * PI * (r * r - mn * mn));
    } else if (r < mx) {
        double q = PI / 3 - acos(sqrt(3) * a / (6 * sqrt(r * r - mn * mn)));
        double s1 = (r * r - mn * mn) * sin(q) * cos(q);
        double s2 = sqrt(3) * (r * r - mn * mn) * sin(q) * sin(q);
        double s3 = q * (r * r - mn * mn);
        printf("%.5f\n", sqrt(3) * a * a - 12 * (s1 + s2 - s3));
    } else printf("%.5f\n", sqrt(3) * a * a);
    return 0;
}