题目链接
Alice 和 Bob 共有一个无向图,其中包含 n 个节点和 3 种类型的边:
- 类型 1:只能由 Alice 遍历。
- 类型 2:只能由 Bob 遍历。
- 类型 3:Alice 和 Bob 都可以遍历。
给你一个数组 edges ,其中 edges[i] = [typei, ui, vi] 表示节点 ui 和 vi 之间存在类型为 typei 的双向边。请你在保证图仍能够被 Alice和 Bob 完全遍历的前提下,找出可以删除的最大边数。如果从任何节点开始,Alice 和 Bob 都可以到达所有其他节点,则认为图是可以完全遍历的。
返回可以删除的最大边数,如果 Alice 和 Bob 无法完全遍历图,则返回 -1 。
示例 1:
1
2
3
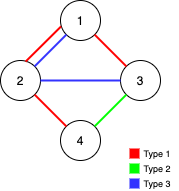
| 输入:n = 4, edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]]
输出:2
解释:如果删除 [1,1,2] 和 [1,1,3] 这两条边,Alice 和 Bob 仍然可以完全遍历这个图。再删除任何其他的边都无法保证图可以完全遍历。所以可以删除的最大边数是 2 。
|
示例 2:
1
2
3
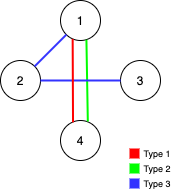
| 输入:n = 4, edges = [[3,1,2],[3,2,3],[1,1,4],[2,1,4]]
输出:0
解释:注意,删除任何一条边都会使 Alice 和 Bob 无法完全遍历这个图。
|
示例 3:
1
2
3
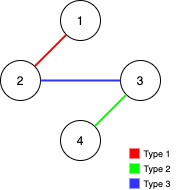
| 输入:n = 4, edges = [[3,2,3],[1,1,2],[2,3,4]]
输出:-1
解释:在当前图中,Alice 无法从其他节点到达节点 4 。类似地,Bob 也不能达到节点 1 。因此,图无法完全遍历。
|
这题就是比较简单的并查集,我们分别对两个人建立一个并查集,先删公共边中的累赘边,再分别删各自独占边中的累赘边即可,AC代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
| class Unionset {
public:
vector<int> father;
vector<int> sum;
int cnt = 0;
public:
void init(int n) {
father.resize(n);
for (int i = 0; i < n; i++) father[i] = i;
sum.resize(n);
cnt = n;
}
int findFather(int x) {
return x == father[x] ? x : father[x] = findFather(father[x]);
}
bool Union(int x, int y) {
x = findFather(x), y = findFather(y);
if (x == y) return 0;
if (sum[x] < sum[y]) swap(x, y);
father[y] = x;
sum[x] += sum[y];
--cnt;
return 1;
}
};
class Solution {
public:
int maxNumEdgesToRemove(int n, vector<vector<int>> &edges) {
Unionset a = Unionset();
Unionset b = Unionset();
int ans = 0;
a.init(n);
b.init(n);
for (auto &i:edges) --i[1], --i[2];
for (auto &i:edges) {
if (i[0] == 3) {
if (!a.Union(i[1], i[2])) ans++;
else b.Union(i[1], i[2]);
}
}
for (auto &i:edges) {
if (i[0] == 1) {
if (!a.Union(i[1], i[2])) ans++;
}
if (i[0] == 2) {
if (!b.Union(i[1], i[2])) ans++;
}
}
if (a.cnt != 1 || b.cnt != 1) return -1;
return ans;
}
};
|


