题目链接
在由 1 x 1 方格组成的 N x N 网格 grid 中,每个 1 x 1 方块由 /、\ 或空格构成。这些字符会将方块划分为一些共边的区域。
(请注意,反斜杠字符是转义的,因此 \ 用 \\ 表示)。
返回区域的数目。
示例 1:
1
2
3
4
5
6
7
| 输入:
[
" /",
"/ "
]
输出:2
解释:2x2 网格如下:
|
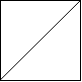
示例 2:
1
2
3
4
5
6
7
| 输入:
[
" /",
" "
]
输出:1
解释:2x2 网格如下:
|
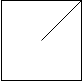
示例 3:
1
2
3
4
5
6
7
8
| 输入:
[
"\\/",
"/\\"
]
输出:4
解释:(回想一下,因为 \ 字符是转义的,所以 "\\/" 表示 \/,而 "/\\" 表示 /\。)
2x2 网格如下:
|
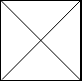
示例 4:
1
2
3
4
5
6
7
8
| 输入:
[
"/\\",
"\\/"
]
输出:5
解释:(回想一下,因为 \ 字符是转义的,所以 "/\\" 表示 /\,而 "\\/" 表示 \/。)
2x2 网格如下:
|
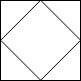
示例 5:
1
2
3
4
5
6
7
| 输入:
[
"//",
"/ "
]
输出:3
解释:2x2 网格如下:
|
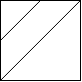
思维+并查集~
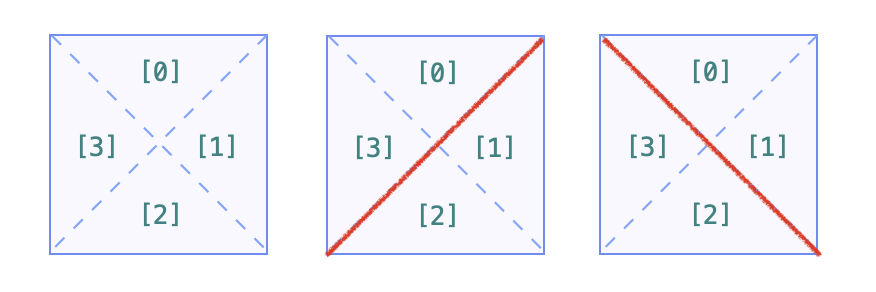
我们可以将一格分成四块,那么对每一格的划分就有下面三张情况,合并对应的编号即可:
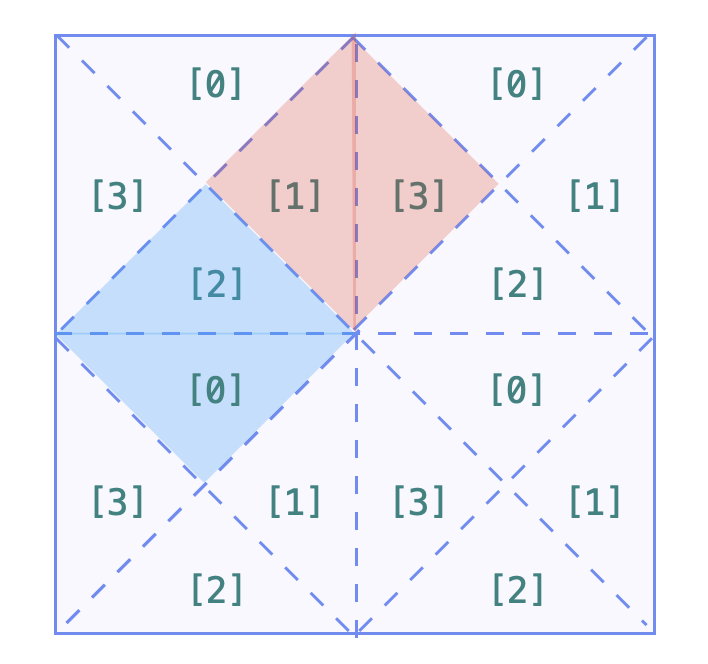
对每一个大格,只有两种相邻情况,合并相应的编号即可:
最后返回连通块的数目即可~
离散化处理:初始化连通块数目置为 $4NN$,将二维坐标离散成一维,$(x,y)->4(xN+y)$
AC代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
| class Unionset {
public:
vector<int> father;
vector<int> sum;
int cnt = 0;
public:
void init(int n) {
father.resize(n);
for (int i = 0; i < n; i++) father[i] = i;
sum.resize(n);
cnt = n;
}
int findFather(int x) {
return x == father[x] ? x : father[x] = findFather(father[x]);
}
bool Union(int x, int y) {
x = findFather(x), y = findFather(y);
if (x == y) return 0;
if (sum[x] < sum[y]) swap(x, y);
father[y] = x;
sum[x] += sum[y];
--cnt;
return 1;
}
};
class Solution {
public:
int regionsBySlashes(vector<string> &grid) {
int N = grid.size();
Unionset u = Unionset();
u.init(4 * N * N);
for (int i = 0; i < N; i++) {
for (int j = 0; j < grid[i].size(); j++) {
int id = 4 * (i * N + j);
if (grid[i][j] == '/') {
u.Union(id, id + 3);
u.Union(id + 1, id + 2);
} else if (grid[i][j] == '\\') {
u.Union(id, id + 1);
u.Union(id + 2, id + 3);
} else {
u.Union(id, id + 1);
u.Union(id + 1, id + 2);
u.Union(id + 2, id + 3);
}
if (i + 1 < N) {
u.Union(id + 2, 4 * ((i + 1) * N + j));
}
if (j + 1 < N) {
u.Union(id + 1, 4 * (i * N + j + 1) + 3);
}
}
}
return u.cnt;
}
};
|






