旺崽的博客

要么天赋异禀，要么天道酬勤

0%

LeetCode 2641 二叉树的堂兄弟节点 II

发表于 更新于 分类于 Valine：

题目链接

给你一棵二叉树的根 root ，请你将每个节点的值替换成该节点的所有 堂兄弟节点值的和 。

如果两个节点在树中有相同的深度且它们的父节点不同，那么它们互为 堂兄弟 。
请你返回修改值之后，树的根 root 。
注意，一个节点的深度指的是从树根节点到这个节点经过的边数。

示例 1：

在这里插入图片描述

1
2
3
4
5
6
7
8
9
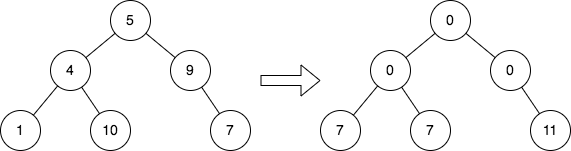
输入：root = [5,4,9,1,10,null,7]
输出：[0,0,0,7,7,null,11]
解释：上图展示了初始的二叉树和修改每个节点的值之后的二叉树。
- 值为 5 的节点没有堂兄弟，所以值修改为 0 。
- 值为 4 的节点没有堂兄弟，所以值修改为 0 。
- 值为 9 的节点没有堂兄弟，所以值修改为 0 。
- 值为 1 的节点有一个堂兄弟，值为 7 ，所以值修改为 7 。
- 值为 10 的节点有一个堂兄弟，值为 7 ，所以值修改为 7 。
- 值为 7 的节点有两个堂兄弟，值分别为 1 和 10 ，所以值修改为 11 。

示例 2：

在这里插入图片描述

1
2
3
4
5
6
输入：root = [3,1,2]
输出：[0,0,0]
解释：上图展示了初始的二叉树和修改每个节点的值之后的二叉树。
- 值为 3 的节点没有堂兄弟，所以值修改为 0 。
- 值为 1 的节点没有堂兄弟，所以值修改为 0 。
- 值为 2 的节点没有堂兄弟，所以值修改为 0 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def replaceValueInTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        q = deque([root])
        cnt = Counter()  # 存当前节点所有儿子节点的值的和
        father = dict()  # 存每个节点的父亲节点
        father[root] = 0  # 根节点的父亲节点
        cnt[0] = root.val
        while q:
            tmp = q
            q = []
            s = sum(node.val for node in tmp)  # 求当前层所有节点的值的和
            for node in tmp:
                if node.left:
                    cnt[node] += node.left.val
                    father[node.left] = node
                    q.append(node.left)
                if node.right:
                    cnt[node] += node.right.val
                    father[node.right] = node
                    q.append(node.right)
                node.val = s - cnt[father[node]]
        return root