旺崽的博客

要么天赋异禀，要么天道酬勤

0%

LeetCode 2642 设计可以求最短路径的图类

发表于 分类于 Valine：

题目链接

给你一个有 n 个节点的 有向带权 图，节点编号为 0 到 n - 1 。图中的初始边用数组 edges 表示，其中
edges[i] = [fromi, toi, edgeCosti] 表示从 fromi 到 toi 有一条代价为 edgeCosti 的边。

请你实现一个 Graph 类：

  • Graph(int n, int[][] edges) 初始化图有 n 个节点，并输入初始边。
  • addEdge(int[] edge) 向边集中添加一条边，其中 edge = [from, to, edgeCost]
    。数据保证添加这条边之前对应的两个节点之间没有有向边。
  • int shortestPath(int node1, int node2) 返回从节点 node1 到 node2 的路径 最小 代价。如果路径不存在，返回
    -1 。一条路径的代价是路径中所有边代价之和。
    示例 1：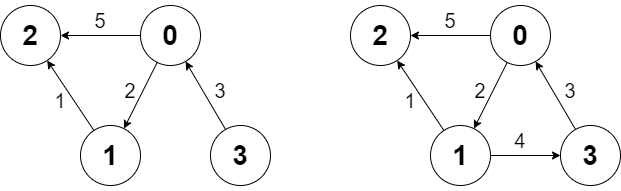
    在这里插入图片描述
1
2
3
4
5
6
7
8
9
10
11
12
输入：
["Graph", "shortestPath", "shortestPath", "addEdge", "shortestPath"]
[[4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]], [3, 2], [0, 3], [[1, 3, 4]], [0, 3]]
输出：
[null, 6, -1, null, 6]

解释：
Graph g = new Graph(4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]);
g.shortestPath(3, 2); // 返回 6 。从 3 到 2 的最短路径如第一幅图所示：3 -> 0 -> 1 -> 2 ，总代价为 3 + 2 + 1 = 6 。
g.shortestPath(0, 3); // 返回 -1 。没有从 0 到 3 的路径。
g.addEdge([1, 3, 4]); // 添加一条节点 1 到节点 3 的边，得到第二幅图。
g.shortestPath(0, 3); // 返回 6 。从 0 到 3 的最短路径为 0 -> 1 -> 3 ，总代价为 2 + 4 = 6 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Graph:
    def __init__(self, n: int, edges: List[List[int]]):
        self.n = n
        self.graph = [[] for _ in range(n)]  # 邻接表
        for u, v, c in edges:
            self.graph[u].append((v, c))

    def addEdge(self, edge: List[int]) -> None:
        u, v, c = edge
        self.graph[u].append((v, c))

    def shortestPath(self, node1: int, node2: int) -> int:
        dist = [-1] * self.n  # 最短距离数组，初始为-1
        dist[node1] = 0
        visited = [False] * self.n  # 记录节点是否被访问过
        pq = [(0, node1)]  # 小根堆，记录最短距离和节点编号
        while pq:
            cur_dist, cur_node = heapq.heappop(pq)
            if visited[cur_node]:  # 跳过已经访问过的节点
                continue
            visited[cur_node] = True
            if cur_node == node2:  # 找到终点，直接返回
                return dist[node2]
            for next_node, next_dist in self.graph[cur_node]:
                if visited[next_node]:  # 跳过已经访问过的节点
                    continue
                if dist[next_node] == -1 or cur_dist + next_dist < dist[next_node]:
                    dist[next_node] = cur_dist + next_dist
                    heapq.heappush(pq, (dist[next_node], next_node))
        return -1  # 没有找到路径