LeetCode 2646 最小化旅行的价格总和

题目链接

现有一棵无向、无根的树，树中有 n 个节点，按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。

每个节点都关联一个价格。给你一个整数数组 price ，其中 price[i] 是第 i 个节点的价格。

给定路径的 价格总和 是该路径上所有节点的价格之和。

另给你一个二维整数数组 trips ，其中 trips[i] = [starti, endi] 表示您从节点 starti 开始第 i 次旅行，并通过任何你喜欢的路径前往节点 endi 。

在执行第一次旅行之前，你可以选择一些 非相邻节点 并将价格减半。

返回执行所有旅行的最小价格总和。

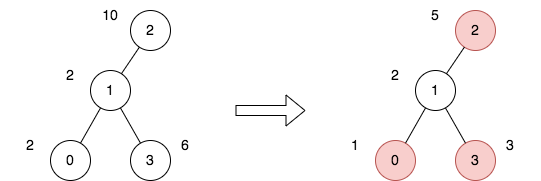
示例 1：

输入：n = 4, edges = [[0,1],[1,2],[1,3]], price = [2,2,10,6], trips = [[0,3],[2,1],[2,3]]
输出：23
解释：
上图表示将节点 2 视为根之后的树结构。第一个图表示初始树，第二个图表示选择节点 0 、2 和 3 并使其价格减半后的树。
第 1 次旅行，选择路径 [0,1,3] 。路径的价格总和为 1 + 2 + 3 = 6 。
第 2 次旅行，选择路径 [2,1] 。路径的价格总和为 2 + 5 = 7 。
第 3 次旅行，选择路径 [2,1,3] 。路径的价格总和为 5 + 2 + 3 = 10 。
所有旅行的价格总和为 6 + 7 + 10 = 23 。可以证明，23 是可以实现的最小答案。

示例 2：

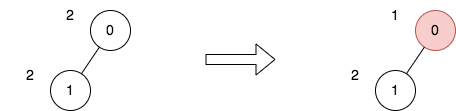
输入：n = 2, edges = [[0,1]], price = [2,2], trips = [[0,0]]
输出：1
解释：
上图表示将节点 0 视为根之后的树结构。第一个图表示初始树，第二个图表示选择节点 0 并使其价格减半后的树。 
第 1 次旅行，选择路径 [0] 。路径的价格总和为 1 。 
所有旅行的价格总和为 1 。可以证明，1 是可以实现的最小答案。

根据最短路径构造一颗新树，然后用树上 DP 求非相邻节点的最大路径和，将这条路径和减半即可得到最终答案：

class Solution:
    def minimumTotalPrice(self, n: int, edges: List[List[int]], price: List[int], trips: List[List[int]]) -> int:
        g = [[] for _ in range(n)]
        for a, b in edges:
            g[a].append((b, price[b]))
            g[b].append((a, price[a]))

        def dijkstra_path(start, end):  # 存储最短路径
            dist = [float('inf')] * n
            dist[start] = 0
            heap = [(0, start, [])]
            while heap:
                d, u, path = heapq.heappop(heap)
                if u == end:
                    return path + [u]
                if d > dist[u]:
                    continue
                for v, w in g[u]:
                    if dist[u] + w < dist[v]:
                        dist[v] = dist[u] + w
                        heapq.heappush(heap, (dist[v], v, path + [u]))
            return []

        price_n = [0] * n
        for s, e in trips:
            path = dijkstra_path(s, e)
            for node in path:
                price_n[node] += price[node]
        dp = [[0] * 2 for _ in range(51)]
        for i in range(n):
            dp[i][1] = price_n[i]

        def dfs(x, f):
            for y, _ in g[x]:
                if y != f:
                    dfs(y, x)
                    dp[x][1] += dp[y][0]
                    dp[x][0] += max(dp[y][1], dp[y][0])

        dfs(0, -1)
        return sum(price_n) - max(dp[0][0], dp[0][1]) // 2